Linear Regression

Reference

Application: testing of treatment effects while adjusting for pre-treatment covariables.

Consider the arrival of a new experimental unit \(n\). This unit has a pre-treatment measurement \(x_n \in \mathbb{R}\) and is assigned a treatment \(z_n \in \{0, 1\}\). After the treatment, the unit produces an outcome

\[ \begin{aligned} y_n = \beta_0 + \beta_1 x_n + \beta_2 z_n + \epsilon_n \\ \epsilon_n \sim N(0, 1). \end{aligned} \]

import numpy as np

size = 5000
np.random.seed(1)
x = np.random.normal(size=size)
z = np.random.binomial(1, 1 / 2, size=size)
epsilon = np.random.normal(size=size)
beta = np.array([1.00, 0.32, 0.16])
y = beta[0] + beta[1] * x + beta[2] * z + epsilon
yx = np.column_stack((y, np.ones(size), x, z))

print(yx)

[[ 1.20608328  1.          1.62434536  1.        ]
 [ 0.61208307  1.         -0.61175641  0.        ]
 [ 1.7668771   1.         -0.52817175  0.        ]
 ...
 [ 2.33983342  1.         -0.77598779  0.        ]
 [-0.85242757  1.          1.08488869  0.        ]
 [ 3.49552322  1.          2.24198946  1.        ]]

We can test the hypothesis

\[ \begin{align} H_0: \beta_2 = 0 \\ H_1: \beta_2 \neq 0 \end{align} \]

and estimate \((1 - \alpha)\) confidence sequences for \(\beta_2\) using a LinearRegression model:

from savvi.linear_regression import LinearRegression

alpha = 0.05
p = beta.size
lr = LinearRegression(alpha, p)

For each new unit sample \(n\), we run the test. If \(p_n(\beta_2) < \alpha\), we have the option to stop running:

sequence = lr.batch(yx)
optional_stop = next(s for s in sequence if s.p_value[2] <= alpha)
optional_stop

Parameter	Estimate	CI Lower	CI Upper	P-value
\(\beta_0\)	1.0056	0.9187	1.1539	0.0
\(\beta_1\)	0.3357	0.2234	0.3987	0.0
\(\beta_2\)	0.2128	0.0027	0.3701	0.0432

Sample size: 949

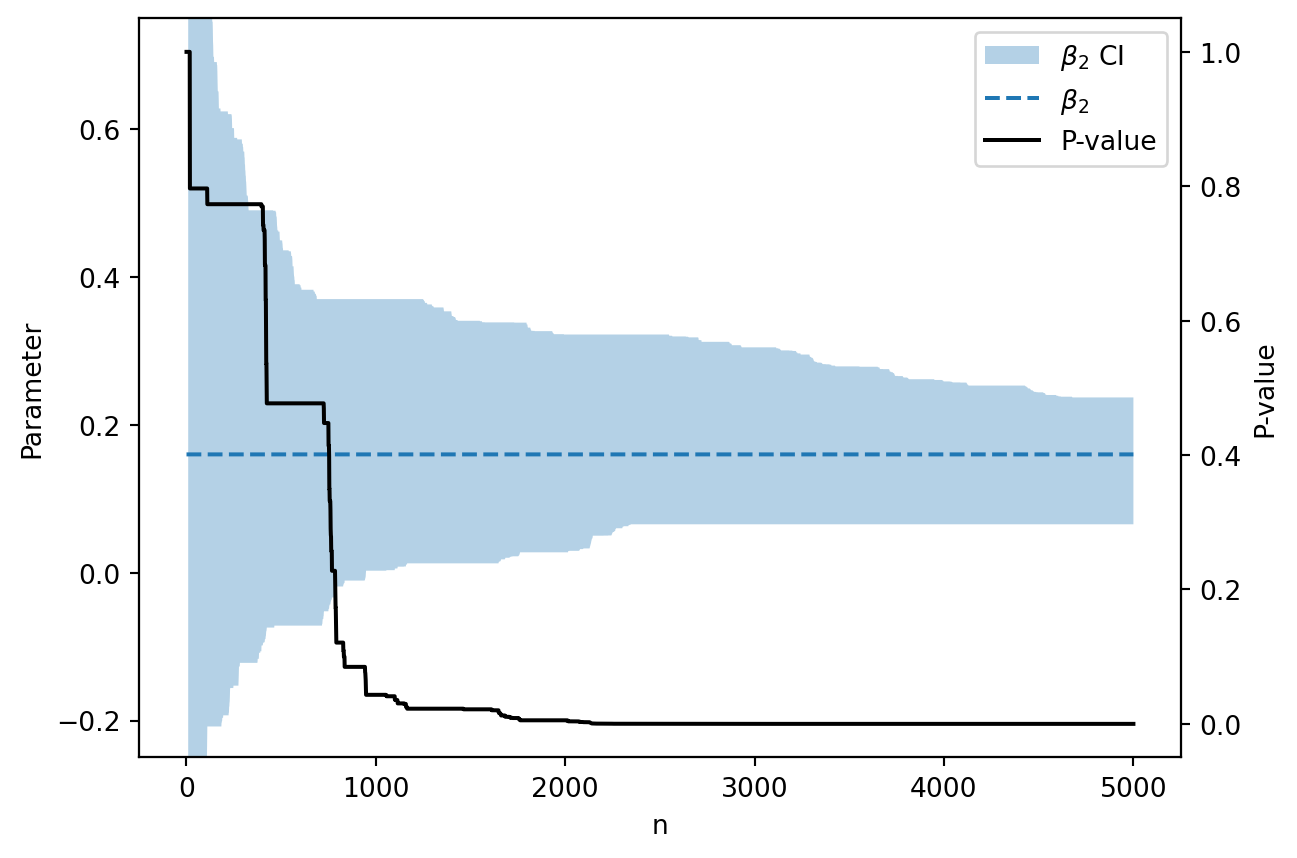
%config InlineBackend.figure_formats = ["svg"]
from savvi.utils import plot

fig, ax1, ax2 = plot(sequence, truth=beta, index=[2])
ax1.set_ylim(-0.25, 0.75)